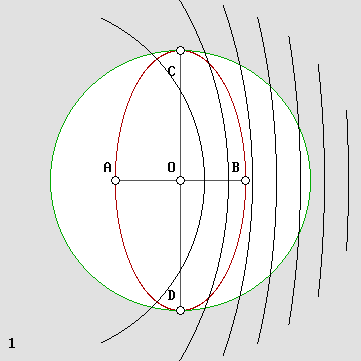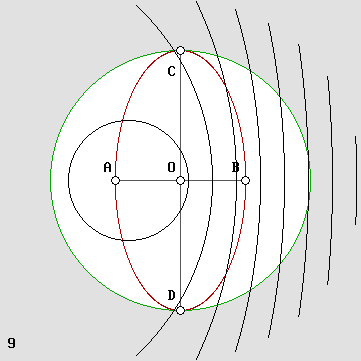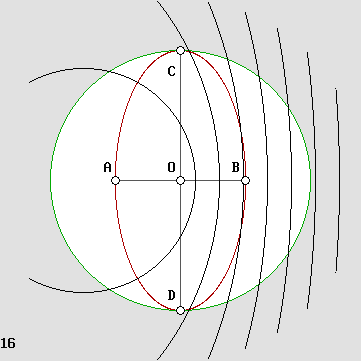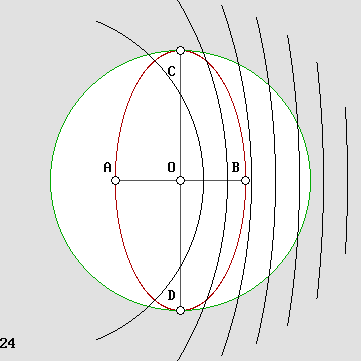
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
THE DOPPLER EFFECT

The Doppler effect explains Relativity.
|
Firstly, let us admit: – All waves need a medium. – The wave speed with respect to the medium is postulated to be constant and absolute, albeit this is true only for the aether. – The phrase "at rest" stands for having no velocity with respect to the medium. Beta. The beta normalized velocity is the speed of the wave source (or observer) as compared to the wave speed. It is very useful in order to make things simpler. Below, v is for velocity and c is the speed of light, albeit c may also stand arbitrarily for the speed of sound.
Lorentz's contraction factor. The contraction factor is given by: g = sqr(1 – beta ^ 2). Henri Poincare called this important, indeed capital phenomenon, "the aberration". The well known gamma factor is the reciprocal: gamma = 1 / g. Apparently, this aberration was discovered by A. A. Michelson. Let us consider a plane constantly flying at 50% of the speed of sound, hence beta = .5 with respect to air. Then the wind speed has an additional effect on the plane with respect to the ground. It may severely modify its relative speed on a round trip flight. It turns out that planes flying across the wind are slowed down according to g. The mean speed in the direction of the wind on a go and return trip is even more severely reduced according to g squared. For more details, see the Michelson Interferometer. However, the problem involving light waves and the aether was solved incorrectly by Michelson. The point is that the normal Doppler effect involves a transverse wavelength contraction according to g and a longitudinal contraction according to g squared. Lorentz finally found that the emitter frequency should slow down according to g. On the one hand, this cancels the transverse contraction. On the other hand, it also reduces the longitudinal contraction from g squared to g. In such a case, assuming that the Michelson interferometer undergoes a contraction according to g along the displacement axis x only, there is no speed or wavelength difference between the two light paths and the interferometer cannot reveal the aether wind any more. So this contraction factor should not be underestimated. It is of the utmost importance. |
1 – THE REGULAR DOPPLER EFFECT
The emitter is moving and the observer is at rest.
The unmoving axis joins the unmoving observer and the unmoving wave origin.
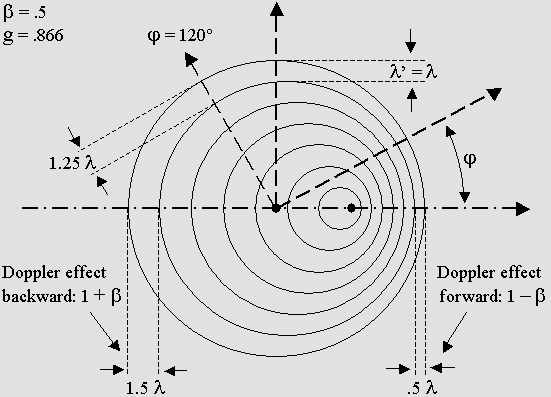

|
Let us take an example for beta = .5 and see how the Doppler effect modifies the sound waves. 1. The forward wavelength is: 1 – beta = .5 times shorter. 2. The backward wavelength is: 1 + beta = 1.5 times longer. 3. The forward frequency is: 1 / (1 – beta) = 2 times higher. 4. The backward frequency is: 1 / (1 + beta) = .6667 times lower. 5. The wavelength for a phi = 120° angle is: 1 – beta * cos 120° = 1.25 times longer. 6. The frequency for a phi = 120° angle is: 1 / (1 – beta * cos 120°) = .8 times lower. 7. The frequency and the wavelength remain unchanged along a transverse unmoving axis. 9. The beta velocity can be deduced from the forward wavelength: beta = 1 – .5 = .5 10. The beta velocity can be deduced from the backward wavelength: beta = 1.5 – 1 = .5 11. The forward vs. backward wavelength or frequency ratio is: R = (1 + beta) / (1 – beta) = 3 12. The beta velocity can be deduced from this ratio: (3 – 1) / (3 + 1) = .5 13. Lorentz's contraction factor is of no interest here: g = sqr(1 – .5 ^ 2) = .866
The observer may use a resonator or a more sophisticated device in order to measure the frequency. Because a plane reflector produces standing waves, he can also measure the wavelength by finding the first node position; this is called the Hertz test. In this case, the observer obtains correct data because he is at rest. This does not mean that an observer at rest always obtain correct data. Astronomers are aware that, even at theoretical rest, a telescope cannot produce an exact image of both Mars and Jupiter. The results must still be interpreted because the speed of light is not infinite. So, dealing in addition with the Doppler effect, one should be even more careful. A moving observer encounters phenomena which are definitely not well understood. This explains why Relativity is not well understood either. My experience with so many readers since over six years is that they never accept to sit down and examine the problem carefully. It is all about laziness, and it is a shame because the calculus is simple. It never needs sophisticated equations. The Voigt transformations. One can use Woldemar Voigt's transformations (1887) in order to reproduce the normal Doppler effect because his equation set can reproduce any Doppler effect including the Lorentz transformations. Below is a reproduction of Poincaré's version of the Voigt transformations in his book "La mécanique nouvelle" (New Mechanics). They are the equivalent of Lorentz's ones and they where intended to cancel the Doppler effect on Maxwell's equations:
This is Poincaré's version of Voigt's equations. k stands for gamma = 1 / g, epsilon for beta and l for Voigt's constant.
One may reverse Voigt's equations like this for the computer in order to produce a Doppler effect instead of canceling it: x' = x * g * k + t * beta t' = t * g / k – x * beta y' = y * k y' = y * k Woldemar Voigt's variable Doppler equations. k stands for Voigt's constant, whose goal is to obtain a variable transverse and longitudinal contraction.
Voigt's constant k must equal Lorentz's factor g in order to obtain the normal g squared axial contraction: k * g = g ^ 2. This is the regular Doppler effect, which then can be reproduced using simpler equations (this is also the case for the Lorentz transformations where k = 1 can be simply removed). x' = x * g ^ 2 + t * beta t' = t – x * beta y' = y * g y' = y * g Woldemar Voigt's equations for the regular Doppler effect.
This is not a joke. Voigt's equations for the regular Doppler effect work beautifully, and I am rather surprised that they are still ignored. x stands for wavelength and t stands for the wave period in radians (not space and time!). The program below shows that they even reproduce the emitter's displacement: Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe |
2 – THE VIRTUAL DOPPLER EFFECT
The observer is moving and the emitter is at rest.
|
There is no true Doppler effect because waves remain unchanged. The experimented observer is aware that his moving instruments cannot correctly record the frequency any more. However, if he already knows its original value, he can deduce his speed from it by means of formulas below. The reception rate slows down if the observer is moving away from source. It rather accelerates if he is moving towards the source. The virtual apparent frequency is given by: The observer is moving towards the source: f ' = f (1 + beta) The observer is moving away from the source: f ' = f (1 – beta) The observer is moving according to a phi angle (all azimuth): f ' = f (1 – beta cos phi)
Let us take an example for beta = .5 and see how the virtual Doppler effect seems to modify the frequency, which actually remains unchanged. 1. The frequency while moving towards the source seems to be 1 + beta = 1.5 times higher. 2. The frequency while moving away from the source seems to be 1 – beta = .5 time lower. 3. The frequency for a phi = 120° angle seems to be: 1 – beta cos 120° = 1.25 times higher. Obviously, there are no wavelength equations because it also remains unchanged. In addition, a moving observer cannot measure the wavelength correctly by means of the Hertz test because the standing wave contraction. Please note that the Hertz test doesn't yield the correct wavelength here because the reflector is moving. Reflected waves are compressed or dilated two times in cascade and a standing wave compression or dilation occurs. So, if the observer knows the original wavelength, he can deduce his speed from the Hertz test. This also works for the relative Doppler effect below, which in this case always causes a longitudinal standing wave compression according to g squared, and a transverse compression according to g. But this absolutely does not work for the Lorentz "relativistic" Doppler effect (scroll down) because the apparatus compression (Lorentz's on-axis matter compression according to g) matches exactly the standing wave compression and the frequency reduction: g ^ 2 / g = g. So the observer cannot deduce his speed through the aether by means of the Hertz test any more. The Michelson interferometer does not work either for the same reason. |
3 – THE RELATIVE DOPPLER EFFECT (not relativistic)
The emitter and the observer are moving together.
The axis, and especially the transverse one, is moving along with the emitter.
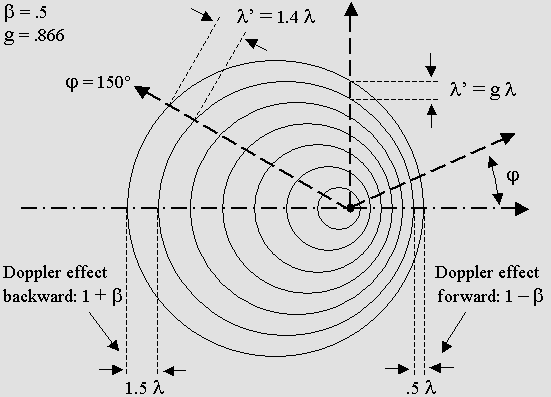
The on-axis relative Doppler effect is identical to the regular one.
I elaborated the first equation below for all-azimuth relative Doppler around 1998.
The second one yields the same results and was adapted from Mr. Ivanov's web site.
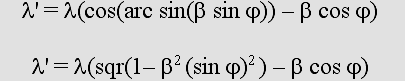
Transverse waves are tilted to an angle from axis: theta = arc sin beta.
Transverse waves (or transverse standing waves) contract according to g.
On-axis standing waves are more severely contracted according to g squared.
|
The important point is that the wavelength here is an artificial one because waves actually propagate from their origin, not from the emitter's new position. Surprisingly, the received frequency is the absolute one: f '' = f whatever the angle. However, the observer should be aware that this happens because he is moving along with the emitter. The sound waves are truly undergoing the Doppler effect, but he cannot detect the frequency change any more because the virtual one cancels the regular one. Let us suppose that beta is .5 and that the observer is placed in front of the emitter. Firstly, the forward true frequency is f ' = f / (1 – beta) = 2 times higher. But the observer is moving away from the place where the sound waves were emitted. So, according to the virtual Doppler effect, he records this truly higher frequency according to f '' = f ' (1 – beta) = .5 time lower. The recorded frequency finally remains unchanged. The equation for this is: f '' = f (1 – beta cos phi) / (1 – beta cos phi), hence f '' = f. This was discovered by Christian Doppler himself in 1842.
Johann Christian Doppler (1803-1853)
The relative but not relativistic Doppler effect applies to any emitting device whose frequency does not slow down according to Lorentz. For example, light emitted by a very distant and fast galaxy does not behave this way because it is submitted to the Lorentz transformations (see the Lorentz Doppler effect below). But the sound emitted by the ambulance siren does, as long as the observer is moving at the same speed and in the same direction. Please note that, for calculation purpose, the transverse axis where x = 0 follows the source. This is Galileo's Relativity Principle. It should be emphasized that the Hertz test still reveals standing waves, hence moving nodes and antinodes. This is possible because the wave relative speed is no longer the same forward and backward. Surprisingly, the wavelength given by the Hertz test will reveal a contraction, which occurs on all x, y and z Cartesian axes. It is given by Lorentz's g factor on a transverse y or z axis and by g squared on the displacement x axis. Michelson was unaware of standing wave contraction, but the contraction ratio is nevertheless consistent with is calculus.
Standing waves motion and contraction. As far as I know, "moving" standing waves were discovered by Mr. Yuri Ivanov. He called them "lively standing waves". He also discovered that a transverse contraction according to g and an on-axis contraction according to g squared occur. He finally used this to explain matter contraction. This was indeed a giant step in physics. Unfortunately, the "Ivanov transformations" are too severe as compared to the correct Lorentz ones. Even worse, his web site about "rythmodynamics", spider-effect and levitation is rather weird. |
4 – THE LORENTZ DOPPLER EFFECT
formerly RELATIVISTIC
The electron frequency slows down according to Lorentz's contraction factor g.
|
This very special Doppler effect is well known, albeit it has been severely misinterpreted and underestimated. It is most often called "relativistic". However, it was discovered by Lorentz, who deserves to have it named after him. In addition, it definitely cannot be called "relativistic" because it is rather absolute: the electron really behaves like this as a result of its true and absolute speed through the aether. So let us call it the Lorentz Doppler effect.
All azimuth Lorentz's Doppler.
On-axis wavelength contraction forward.
On-axis wavelength dilation backward.
The electron frequency slows down according to g. There is no transverse wavelength contraction any more: lambda' = lambda. This alone explains the Lorentz transformations and Relativity. So let me introduce the "formula of the century": |
|
f ' = g f |
The electron frequency slows down according to g.
This produces a very special Doppler effect.
It transforms matter in such a way that the observer's speed becomes unnoticeable.
This, and only this, explains Relativity.
|
Lorentz discovered matter contraction, but he also very clearly stated that matter should not contract on transverse y and z axes. In addition, he strongly believed that there was an aether and he was well aware that the light waves should undergo this special Doppler effect involving no transverse contraction. Finally, the only useful information to be remembered from his famous transformations is the constant transverse length or wavelength: y' = y z' = z As a result of the normal Doppler effect, waves are more contracted forward than they are dilated backward. But here the forward contraction is always the reciprocal of the backward dilation. This leads to Lorentz's Relativity. For example, a 1000 Hz loudspeaker moving at 60% of the speed of sound (beta = .6; g = .8) produces the regular asymmetric Doppler effect: Regular Doppler forward frequency: 1000 / (1 – .6) = 2500 Hz Regular Doppler backward frequency: 1000 / (1 + .6) = 625 Hz A perfect symmetry. However, a 1000 MHz antenna at rest will rather emit at 800 MHz while moving at 60% of the speed of light in accordance with Lorentz's g factor. This will produce a very special Doppler effect: Lorentz "relativistic" Doppler forward: .8 * 1000 / (1 – .6) = 2000 MHz Lorentz "relativistic" Doppler backward: .8 * 1000 / (1 + .6) = 500 MHz As compared to the antenna at rest, the forward frequency will be 2000 MHz, two times higher, while the backward frequency will be two times slower: 500 MHz. A unique wavelength or frequency ratio appears (R = 2 here) for either backward (redshift) or forward (blueshift) waves. The forward ratio is the reciprocal of the backward one, so ratios smaller then 1 can be converted to 1 / R in order to normalize R > 1.
For example, a distant galaxy whose speed is 90% of the speed of light (beta = .9 and g = .4359) exhibits a redshift ratio R = 4.359 which is incompatible with the regular 1+beta Doppler because the maximum possible should be 2. This indicates that the emitted frequency really slows down according to Lorentz's predictions. This calculus would be perfectly true only if our galaxy was at rest with respect to the aether. But it still works because the law of Relativity indicates that all seems to happen as if the observer was truly at rest. In my opinion, astronomers and astrophysicists should admit that the formula beta = 1–2/(R^2+1) shown above is consistent with Lorentz's point of view. They should also admit that fast moving galaxies are (or seem) more and more compressed, and this includes distances between them. So, if Lorenz was right, there is a sort of "time wall" over there: beyond that point, no matter could exist because it would be faster than the speed of light. So the Hubble constant should also be tempered according to g. In brief, the universe would be finite. The "time wall" would stand very near to where our biggest telescopes can already see. As a matter of fact, the Hubble telescope could see very distant and fast moving galaxies. However, this does not appear likely. I am of an opinion that the aether itself could rather expand. Then distant galaxies would still be immobile with respect to the aether locally and the Lorentz transformations would not apply. Finally, just the expansion of the universe could totally explain the unusual Doppler effect; but this would also indicate that such galaxies are truly faster than the speed of light with respect to our galaxy. The Lorentz transformations are just a Doppler effect. This can easily be demonstrated because Lorentz borrowed his equations from Woldemar Voigt, whose goal in 1887 was to cancel the Doppler effect on Maxwell's equations. In addition, I could reverse Lorentz's equations, and the result is a set which produces a Doppler effect instead of canceling it:
Lorentz's Doppler equations.
The first equation needs further explanation. Firstly, swapping x and x' variables cancels the Doppler effect instead of producing it: x = g * x' + beta * t Extracting x' variable: x' = (x – beta * t) / g Also, g =sqr(1 – beta ^ 2): x' = (x – beta * t) / sqr(1 – beta ^ 2) Here, t and t' stand for seconds or wave periods. However this equation uses wavelength or light-second units for x and x'. Beta and x can be converted into any other speed or distance units, and the final result is Lorentz's original equation: x' = (x – v t) / sqr(1 – (v / c) ^ 2) Reciprocity. It turns out that the Lorentz transformations are just a Doppler effect. Nothing else. Nothing more. Henri Poincare discovered that Lorentz's equations could be reversed in a very unusual way, just using the plus sign instead of the minus sign, actually the same way as Descartes did for Galileo's Relativity principle. Galileo: x' = x + v t Reversed: x = x' – v t Poincare: x' = gamma * (x + beta * t) Reversed: x = gamma * (x' – beta * t')
Mathematically, x should rather be recovered like this, using t instead of t': x = x' / gamma – beta * t Surprisingly, the symmetric equations can either produce or correct the Doppler effect. Poincare had discovered Relativity and he was the first person to use this word, well before Einstein. However, his equations only show that a moving observer will be fooled. One cannot freely use two different space or time units without any preference because facts are absolute. Facts are not what they look like, they are what they are. The program Ether17.exe (source code Ether17.bas) reproduces the Lorentz Doppler effect using solely Lorentz's equations. And this especially applies to the electron, simply because its frequency slows down according to g. This is a flawless demonstration. So there is no space-time transformation, just a Doppler transformation involving a wave position according to x' and a wave phase according to t'. The program below is even more explicit because one can test up to four different constants. Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe Matter contraction. It is a well known fact that the electron is responsible for molecule binding, and that it behaves in accordance with a given wavelength. The point is: the electron is submitted to Lorentz's Doppler effect. Because Relativity has been demonstrated hundreds of times, the moving electron must undergo a Doppler effect and transform the way Lorentz predicted. So matter must contract on the Cartesian x axis, but not on transverse y and z axes. Exactly the way the electron standing waves do. Relativity. The consequence of this is that a moving observer becomes unable to determine whether he is moving or not. Because of Lorentz's Doppler perfect symmetry, and because he himself is transformed, he will rather think that an emitter at rest is moving. This reproduces Galileo's Relativity Principle. It is absolutely amazing. It must be emphasized that the moving observer is wrong. Only the observer at rest is right. The stunning reciprocity between their calculations proves that Relativity is true, but there is no true reciprocity. This also proves that Relativity is compatible with the existence of the aether. Active and reactive mass. Lorentz also discovered that mass should increase in accordance with the gamma factor. One can easily prove that the Doppler effect is responsible for this. The Lorentz Doppler effect is involved here, so the electron slower frequency according to g must be taken into account. A slower frequency means less energy, but in spite of that the overall result will rather be a mass/energy gain. The mass is divided into two parts. The part moving forward is active and the backward one is reactive. Firstly, they both are reduced according to g. Secondly, they are transformed according to the Doppler effect.
Active and reactive mass. The action and reaction law is just a consequence of the Lorentz Doppler effect.
Let us take an example for beta = .866; g = .5; gamma = 2; m = 1. The results are undisputable. The sum a + r is consistent with Lorentz's predictions, which have been thoroughly verified nowadays. Active mass: a = 1.866 kg Reactive mass: r = .134 kg. Total mass M = a + r = gamma * m M = 1.866 + .134 = 2 kg.
The action and reaction law. In addition, active and reactive mass is responsible for action and reaction. A billiard ball can push another one simply because its waves undergo the Doppler effect. It turns out that the mass gain is pure kinetic energy. E = (a + r – m) c 2 = (gamma * m – m) c 2 The Time Scanner. In March 2004, I invented a stunning device which I called the Time Scanner. On the one hand, it can reproduce the electron unusual Doppler effect involving a slower frequency. On the second hand, it can perform multiple Lorentz transformations in a single step! |
|
|
The Lorentz transformations are directly linked to the electron Doppler effect.
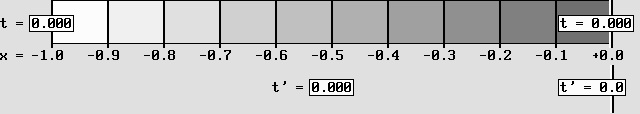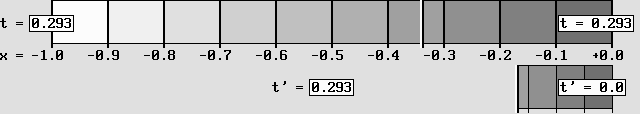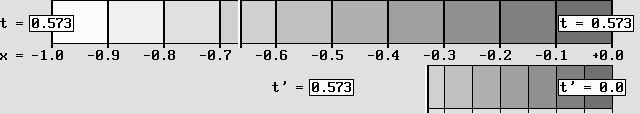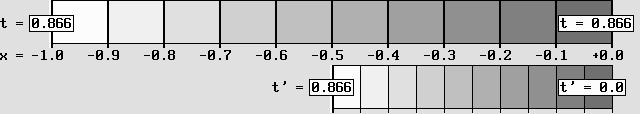
The Time Scanner produces a contraction, a time dilation and a time shift.
Scanning in the opposite direction rather cancels those effects: the Reciprocity works here too.

Here, a system at rest (on the left) is accelerated to .866 c.
This is how a rotating wheel and its different gear systems would look like.
Lorentz's equations cannot handle so many transformations simultaneously.
Einstein's Relativity leads to many paradoxes, not to say contradictions.
On the contrary, the Time Scanner is highly versatile, consistent and logical.
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
|
|
Gabriel LaFreniere, Bois-des-Filion in Québec.
On the Internet since September 2002. Last update December 3, 2009. |